Orthy
기술의 놀라운 발전 본문
어제 당직근무를 서면서 Munkres, Topology, Chpt4의 이론 공부와 각 section 별 연습문제 풀이를 모두 마치고,
'Review of the Basics'라는 이름의 supplementary exercise를 해결하기 시작했다.
11시 20분부터 김도영이 나온 전참시를 본방사수하고, 더 공부를 할까 하다가 새벽쯤이 되어선 도저히 집중이 안 되어 공부를 접고 티비만 봤다. '틈만 나면'이라는 프로의 다시보기를 돌려보다가, 특선영화를 보다 보니 비록 피곤에 절었지만 당직철수할 시간이 되었다.
오늘 당직철수 후 1시즈음까지 자고, 일어나 뒹굴거리다 잠시 책상에 앉았다.
R^omega space in the uniform topology의 countability axiom을 점검했다.
- First countable임은 metric space이니 당연하다.
- Second countable이 아님은 p.188의 예시에서 다뤘다.
- Lindelof / separable이 아닐 것 같았는데, 이유를 설명하기 어려워 한참 고민하다 전자는 각 x를 중심으로 하는 r=1/2인 open ball들의 collection이 countable subcover를 가진다고 가정한 뒤 모순을 끌어내는 방법을 써 해결했지만 후자가 해결이 안되어... 인터넷 서칭을 하다 답이 안나와 정말 오랜만에 gpt를 찾았다.
문제를 해결하고 이 다음 목표를 위해 어떻게 공부를 이어나가야 할 지 gpt에게 질문했는데... 답변 수준이 놀랍다.




처음 gpt가 나왔을 때에 비하면... 정말 답변의 수준이 크게 차이난다. 공부를 하는데 있어 좋은 친구가 생긴 것도 같지만, 이렇게 능력이 출중한 ai에 비해 내 수학 능력이 무슨 쓸모가 있을지, 고민하게 된다.
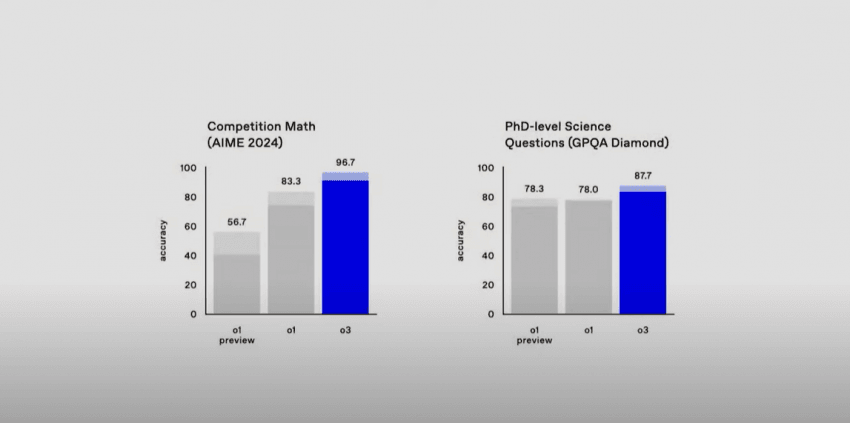
(수스퍼거만) 재밌는 짤도 투척

내일부터 Tychonoff theorem 공부를 시작할 것 같다.
그 후 quotient topology, local connectedness 등을 공부한 뒤에는...
바로 Chpt 9로 넘어가 Algebraic Topology를 공부한다.




