Orthy
Galois Theory (2). Isomorphism Extension Theorem 본문
이제 점점 Galois Theory의 핵심으로 들어간다. 언제나, 우리가 관심있는 대상이 $F$의 확대체 $K$에 대해 $F$를 고정하는 $K$에서의 automorphism임을 기억해두어야 한다.
먼저 Extension Theorem을 소개한다.
$\textbf{Theorem 2.1}$
체 $F$의 한 algebraic extension $E$를 생각하자. $\sigma : F \rightarrow F'$가 isomorphism이라 하자. $F'$의 algebraic closure $\overline{F'}$에 대해, $\sigma$는 $E$에서 $\overline{F'}$의 어떤 subfield로의 isomorphism $\tau$로 'extend' 될 수 있다. 이때 $\tau$가 $\sigma$의 extension이라는 것은 $\tau(a)=\sigma(a), \forall a\in F$를 의미한다.
Extension Theorem은 아래의 그림으로 요약될 수 있다.
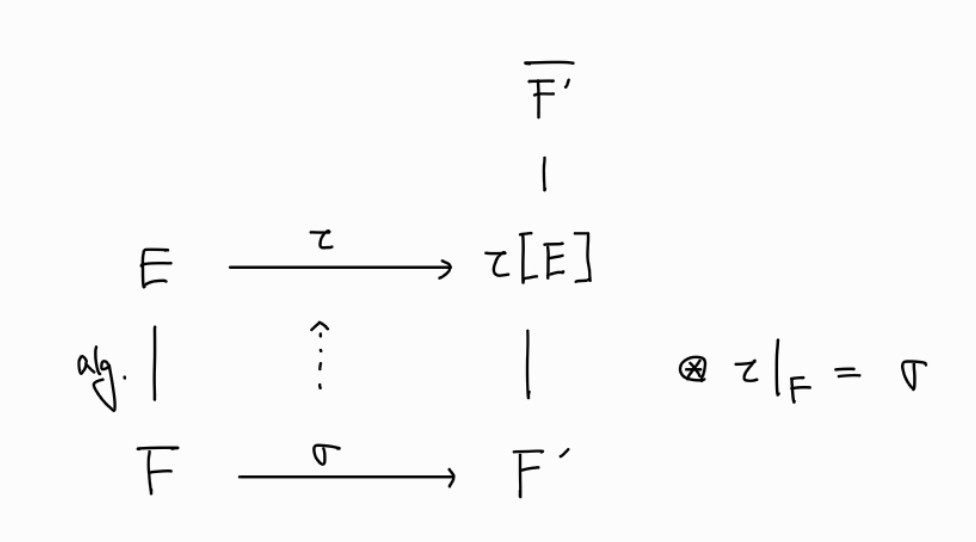
주의해야 할 것은, $\sigma$가 $F$에서 $F'$으로의 isomorphism이지, automorphism이 아니라는 점이다. 마찬가지로, $\tau$ 역시 isomorphism이지 automorphism이 아니다. $\tau$가 $\overline{F'}$의 subfield로 갈 때, 정확히 어떤 subfield로 가는지 이 정리만으로는 말할 수 없다.
물론, 나중에는 $\sigma$ 그리고 특히 $\tau$가 automorphism인 경우를 다룬다. 그러나 이를 위해서는 $E$가 특정한 조건을 만족해야 한다. 어떤 조건을 만족해야 하는지는 Extension Theorem의 증명에서 힌트를 얻을 수 있다.
우리가 먼저 생각할 것은, $F$에서 정의된 $\sigma$를 simple extension field로 extend 하는 경우다. $F$의 원소가 아닌 $\alpha\in E$에 대해, simple extension $F(\alpha)$를 생각하자.
$$p(x)=\mathrm{irr}(\alpha, F)=a_0+a_1 x+\cdots+a_n x^n$$
이라고 하자. 이제 $q(x)=\sigma(a_0)+\sigma(a_1)x+\cdots+\sigma(a_n)x^n$의 한 근 $\beta\in\overline{F'}$를 택할 수 있다. 만약 $q(x)$가 $F'$에서 reducible이면 $\sigma$가 isomorphism이므로 $p(x)$ 역시 $F$에서 reducible이니, $\beta$는 $F'$ 안에 있지 않다. 이제 $\tau : F(\alpha) \rightarrow F'(\beta)$를 생각하면, $\tau$는 우리가 원하는 $\sigma$의 extension이다.
만약 $E=F(\alpha)$이면 Extension Theorem의 증명은 끝이다. 그러나 $E$는 $F$의 임의의 algebraic extension이고, 따라서 완전한 증명을 위해서는 이런 과정을 무한히 반복해야 한다. 여기서 Zorn's Lemma가 사용되어야 함을 이해할 수 있다. 이것이 증명의 아이디어이고, 자세한 증명은 교재를 참고하자.
앞으로 우리가 관심있게 다룰 Extension Theorem의 활용 중 하나는 $F$ 위에서의 automorphism $\sigma$에 대해 $F$의 한 algebraic extension $E$ 위에서 정의된 $\sigma$의 extension $\tau$가 automorphism이 되는 경우이다. 이를 고민하기 위해 $F$의 원소가 아닌 $\alpha\in E$를 생각해보자. $\alpha$는 algebraic over $F$이므로 $p(x)=\mathrm{irr}(\alpha, F)$가 존재한다.
$$p(x)=\mathrm{irr}(\alpha, F)=a_0+a_1 x+\cdots+a_n x^n$$
라 할 때, $\tau(p(\alpha))=a_0+a_1\tau(\alpha)+\cdots+a_n\tau(\alpha)^n=0$이어야 하고, $\tau$가 automorphism이 되기를 바라므로, $\tau(\alpha)\in E$여야 한다. 그런데 $\tau$가 isomorphism이기도 하니, $\tau(\alpha)$와 $\alpha$는 conjugate over $F$이다. 즉, $\alpha$가 $\tau$에 의해 그것의 conjugate로 사상되고 그 conjugate가 E안에 있을 때-다시 말해, $p(x)$의 해가 $E$안에 있을 때, $\tau$는 automorphism이 될 일말의 가능성을 가진다. 이 아이디어는 splitting field를 정의하게 된 이유이며, 필요충분조건에 대해서는 다음 포스팅에서 이야기 할 생각이다.1
Extension Theorem을 공부하는 가장 큰 이유는 이 정리가 $F$를 고정하는 $E$ 위에서의 isomorphism의 개수를 셀 수 있게 해주기 때문이다.
$\textbf{Theorem 2.2}$
체 $F$의 finite extension field $E$를 생각하자. $\sigma : F \rightarrow F'$가 isomorphism이라 하자. $E$에서 $\overline{F'}$의 subfield로의 isomorphism $\tau$가 $\sigma$의 extension일 때, 그러한 $\tau$의 개수는 유한하고 $F$와 $E$에 의해서만 완전히 결정된다.
이 정리는 증명을 보아야 정확히 무슨 말을 하고 있는 것인지 이해할 수 있다.
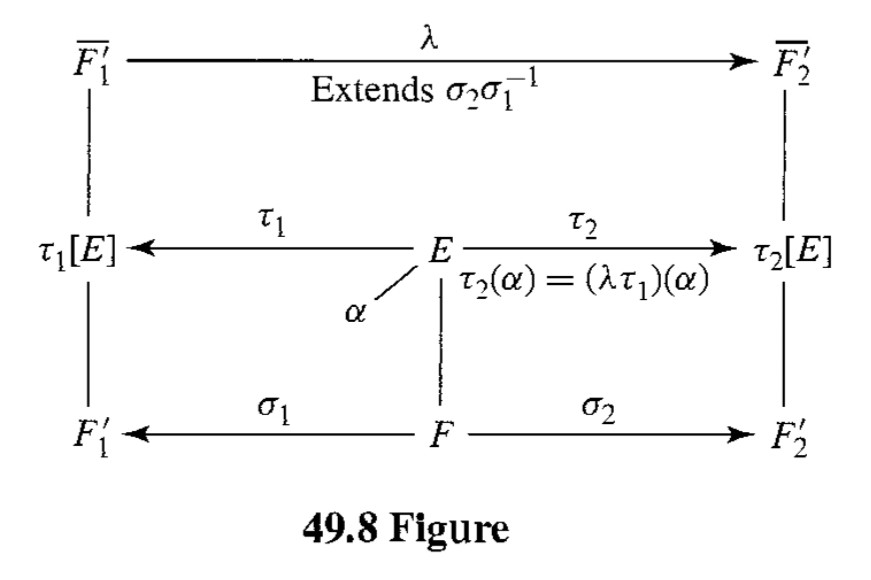
먼저 $\sigma$의 extension $\tau$가 $E$와 $F$에 의해서만 온전히 결정된다는 것을 보이기 위해 $\sigma_1 : F \rightarrow F_1'$와 $\sigma_2 : F \rightarrow F_2'$를 생각한 뒤, Extension Theorem에 의해 이들을 각각 $\tau_1$과 $\tau_2$로 extend하자. 그러면 위의 그림과 같은 상황이 만들어진다.
이제 $\sigma_2\sigma_1^{-1} : F_1' \rightarrow F_2'$를 생각하면 이는 isomorphism이고, 이들 각각의 algebraic closure $\overline{F_1'}$과 $\overline{F_2'}$를 생각하면 이들도 역시 isomorphic이다.2 따라서 $\sigma_2\sigma_1^{-1}$을 $\overline{F_1'}$로 extend해서 얻는 isomorphism $\lambda$는 $\lambda : \overline{F_1'} \rightarrow \overline{F_2'}$이다. 이제 $\lambda\tau_1 : E \rightarrow \overline{F_2'}$는 $\lambda\tau_1=\tau_2$를 만족함을 보일 수 있고, 따라서 $\tau_1$ 하나는 $\tau_2$ 하나를 결정한다. 반대로 $\lambda\tau_2 : E \rightarrow \overline{F_2'}$를 생각하면 비슷하게 $\lambda\tau_2=\tau_1$을 만족함을 보일 수 있고, 따라서 $\tau_2$ 하나는 $\tau_1$ 하나를 결정한다. 즉, $E$에서 정의된 $\overline{F_1'}$의 subfield로의 isomorphism 중 $F_1'$를 고정하는 것들의 모임과 $E$에서 정의된 $\overline{F_2'}$의 subfield로의 isomorphism 중 $F_2'$를 고정하는 것들의 모임 사이에는 일대일 대응이 존재한다. 따라서 $\sigma$의 extension $\tau$가 $E$와 $F$에 의해서만 온전히 결정된다.
$E$는 $F$의 finite extension이므로 $E=F(\alpha_1, \cdots, \alpha_n)$인 $\alpha_1, \cdots, \alpha_n\in E$가 존재하고, $p_i(x)=\mathrm{irr}(\alpha_i, F)$에 대해 $\tau(\alpha_i)$는 $p_i(x)$의 근이어야 하니 가능한 $\tau(\alpha_i)$의 값은 유한하다. 따라서 $E$에서 $\overline{F}$의 subfield로의 isomorphism 중 $F$를 고정하는 것의 개수는 유한하다.(끝)
이때 $E$에서 $\overline{F}$의 subfield로의 isomorphism 중 $F$를 고정하는 것의 개수를 index of $E$ over $F$라 하고, 간단히 $\left\{E : F\right\}$로 나타낸다. 군에서 index란 left coset의 개수인데, $\left\{E : F\right\}$를 index라고 부르는 이유 또한 Galois Theory의 Main Theorem에서 확인할 수 있다.
다음 정리는 index의 정의에 의하면 무척 자명하다.
$\textbf{Theorem 2.3}$
$F\le E\le K$이고 $K$가 $F$의 finite extension field라면 다음이 성립한다.
$$\left\{K : F\right\}=\left\{K : E\right\}\left\{E : F\right\}$$
예시를 살펴보자. $E=\mathbb{Q}(\sqrt{2}, \sqrt{3})$이라 하자. $\left\{E : \mathbb{Q}\right\}$를 구해보자. $\textbf{Theorem 2.3}$에 의하면 $\left\{E : \mathbb{Q}\right\}=\left\{E : \mathbb{Q}(\sqrt{2})\right\}\left\{\mathbb{Q}(\sqrt{2}) : \mathbb{Q}\right\}$이다.
$\left\{\mathbb{Q}(\sqrt{2}) : \mathbb{Q}\right\}$를 구해보자. $\iota : \mathbb{Q}\rightarrow\mathbb{Q}$에 대해, $\mathbb{Q}(\sqrt{2})$에서 $\overline{\mathbb{Q}}$의 subfield로의 isomorphism $\tau$는 $\sqrt{2}$를 어디로 보내느냐에 따라 결정되고, $\tau(\sqrt{2})$는 $\sqrt{2}$와 conjugate over $\mathbb{Q}$이니 $\tau(\sqrt{2})=\pm\sqrt{2}$이다. 따라서 $\left\{\mathbb{Q}(\sqrt{2}) : \mathbb{Q}\right\}=2$이다.
비슷하게 $\left\{E : \mathbb{Q}(\sqrt{2})\right\}$도 $\sqrt{3}$을 어디로 보내느냐에 따라 결정되고, 가능한 것이 $\pm\sqrt{3}$이니 $\left\{E : \mathbb{Q}(\sqrt{2})\right\}=2$이다. 따라서 $\left\{E : \mathbb{Q}\right\}=4$이다.
$E$의 degree of extension $[E : \mathbb{Q}]$를 생각하면, 이 역시 $4$이니 $[E : \mathbb{Q}]=\left\{E : \mathbb{Q}\right\}=4$인데, 이것은 우연이 아니다. 우리가 앞으로 관심있게 볼 extension은 바로 이를 만족하는 특별한 extension $E$이다.
- 지금은 명확하지 않아 보이는 것들도 나중에 가면 명확해진다. 대학 수학을 공부하는데 있어 명심해야 할 것은, 우리는 수학을 '거꾸로' 배우고 있다는 점이다. 수학은 특별한 사례를 일반화/추상화하며 발전한다. 그러나 교과서를 통해 수학을 공부할 때 우리는 반대로 일반화된 정의와 정리를 학습한 다음에야 특별한 사례들을 접하게 된다. 그러면서 사례들을 무시하는 경우가 많은데, 예시에 대한 고민 없이는 정의와 정리를 이해하는 것은 무척 힘들다. [본문으로]
- 이것은 당연한 결과가 아니다. Extension Theorem의 결과로 나오는 것으로, 증명이 궁금한 사람은 https://math.stackexchange.com/questions/2585321/uniqueness-of-algebraic-closure를 참고하면 된다. [본문으로]
'학부 수학 > 현대대수학' 카테고리의 다른 글
| 2023년 2학기 현대대수학2 필기본 (0) | 2025.02.04 |
|---|---|
| [현대대수학1] 10, 11주차 필기 (3) | 2024.11.26 |
| Galois Theory (1). Conjugate Isomorphism Theorem (0) | 2024.01.02 |
| Galois Theory: Preview; The Main Theorem (0) | 2024.01.02 |
| [현대대수학] Field Extension (2) (0) | 2023.10.18 |


