Orthy
Galois Theory: Preview; The Main Theorem 본문
이번 학기 공부한 현대대수학 내용을 스스로 정리하려 올리는 포스팅입니다. Fraleigh의 'Abstract Algebra'로 공부하였으며, Section 48~Section 56의 내용이 메인입니다. 사실 수학과에 진학하고 싶었던 것이 Galois Thoery를 공부하고 싶어서였는데, 부족하게나마 이해를 한 것 같습니다. 아직 갈 길이 멀지만...
Galois Theory는 군과 체 사이의 대칭을 설명하는 이론이다. 이때 '어떤' 군과 '어떤' 체 사이의 대칭에 관심있는지 주목해야 한다. Galois Theory의 핵심은 이 글에서 설명하는 Main Theorem인데, 이를 이해하기 위한 여러 개념들에 앞서 정리를 먼저 소개하는 것이 좋겠다는 생각이 들었다.
대수학은 방정식의 근을 탐구하는 학문이라고 할 수 있다. 고대 그리스, 중동 그리고 중국에서 독립적으로 이차방정식의 해법을 발견한 이후 천 년 이상이 지나 이탈리아의 타르탈리아(Tartaglia)와 카르다노(Cardano)는 삼차방정식의 해법을 발견했고, 카르다노의 제자 페라리(Ferrari)는 사차방정식의 해법을 발견했다.
여기서 방정식의 해법이란 우리가 흔히 '근의 공식'이라 부르는 것으로써, 방정식의 계수를 이용하여 근을 표현하는 것을 의미한다.
예를 들어, 이차방정식 $ax^2+bx+c=0$의 해법-즉 근의 공식은 아래와 같이 주어진다.
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
삼차방정식과 사차방정식의 경우 내가 다시 증명해 보이는 것은 시간낭비이니, 아래 글을 참고하면 된다.
https://wiki.mathnt.net/index.php?title=3%EC%B0%A8_%EB%B0%A9%EC%A0%95%EC%8B%9D%EC%9D%98_%EA%B7%BC%EC%9D%98_%EA%B3%B5%EC%8B%9D
3차 방정식의 근의 공식 - 수학노트
개요 삼차방정식 \(ax^3+bx^2+cx+d=0\) 의 근의 공식 카르다노의 해법 주어진 방정식 \(x^3+ax^2+bx+c=0\)의 2차항을 없애기 위해, 치환 \(x = t - a/3\)을 사용한다. 새로운 방정식 \(t^3 + pt + q = 0\)을 얻는다. 여
wiki.mathnt.net
https://pkjung.tistory.com/163
4차방정식의 해법
이 글은 4차방정식의 해를 구하는 방법을 소개한다. 3차방정식의 해법은 이 블로그의 다음 글을 참고하기 바란다. https://pkjung.tistory.com/158?category=41087 3차방정식의 여러 가지 해법 이 글은 3차방정
pkjung.tistory.com
계수가 실수인 이차, 삼차, 사차방정식은 실수인 근을 가지기도 하지만, 실수가 아닌 근을 가지기도 한다. 이때 우리는 그 근을 허수인 근이라고 부르며, 기존의 수 체계를 실수에서 복소수로 확장하게 된다.
현대대수학 그리고 Galois Theory에서는 이 개념을 추상화하여, 어떤 체 F에 대해 계수가 F의 원소인 다항식 그리고 그 다항식의 근을 생각한다. 이제 F의 한 '확대체', 그러니까 F를 포함하면서 F보다 더 큰 체 K가 있다고 해보자. 앞서 살펴본 예시에서라면, 실수체 $\mathbb{R}$의 확대체로 복소수체 $\mathbb{C}$를 생각할 수 있다.
이제 K에서 자기 자신으로의 자기동형사상(automorphism)1 중 F를 고정하는 것들의 집합을 $G(K/F)$라고 하면 $G(K/F)$는 합성(composition)에 대한 군을 이루고 있음이 자명하다. 그러면 $G(K/F)$의 subgroup과 $F\le E\le K$인 intermediate field E 사이에 모종의 대칭관계가 있을 것이라고 추측2할 수 있다.

위 그림에서 $K_H=\left\{a\in K : \sigma(a)=a, \forall\sigma\in H\right\}$이다.
Main Theorem은 이 관계가 실제로 성립하며, 두 집합 사이에 잘 정의된(well-defined) 일대일 대응이 있음을 알려주는 정리이다. 그리고 이로부터 전개되는 Galois Theory의 결과, 5차 이상의 방정식은 일반화된 해법이 없음을-즉 계수를 이용하여 근을 나타내는 일반적인 공식이 존재하지 않다는 것을 보일 수 있는 것이다.
$\textbf{Theorem}$
$K$가 $F$의 normal extension field라고 하자. 이때 $G(K/F)$를 Galois group of K over F라고 부른다. $F\le E\le K$를 만족하는 체 $E$에 대해, $\lambda(E)$를 $E$를 고정하는 $G(K/F)$의 subgroup이라고 하자. 그러면 $\lambda$는 $F$와 $K$의 모든 intermediate field의 집합에서 $G(K/F)$의 모든 subgroup의 집합으로의 잘 정의된 일대일 대응이며, 다음이 참이다.
(1) $\lambda(E)=G(K/E)$
(2) $E=K_{G(K/E)}=K_{\lambda(E)}$
(3) $H\le G(K/F)$이면 $\lambda(E_H)=H$
(4) $[K : E]=\left|\lambda(E)\right|$이고 $[E : F]=(G(K/F) : \lambda(E))$
(5) $E$가 $F$의 normal extension field일 필요충분조건은 $\lambda(E)$가 $G(K/F)$의 normal subgroup인 것이다. 그리고 그 때, $G(E/F)\simeq G(K/F)/G(K/E)$이다.
(6) $G(K/F)$의 subgroup diagram은 $F$와 $K$ 사이의 intermediate field diagram을 거꾸로 뒤집어 놓은 모양이다.
표기법은 Fraleigh의 'Abstract Algebra'를 따랐다. $[K : E]$는 degree of extension, $(G(K/F) : \lambda(E))$는 the number of left cosets of $\lambda(E)$ over $G(K/F)$이다.
Main Theorem을 통해 $F$와 $K$의 모든 intermediate field의 집합에서 $G(K/F)$의 모든 subgroup의 집합으로의 잘 정의된 일대일 대응을 구축하고자 하는 우리의 목표가 달성되며, 군과 체의 대칭성에 대한 정보를 얻게 되었다.
사실 Main Theorem까지 가는 여정이 다항식의 근을 가지고 있는 체와 한 근에서 다른 근으로 가는 사상(mapping)을 탐구한 것이었음을 곰곰히 생각하면, 곱씹을수록 이러한 대응이 자연스럽게 주어져야만 함을 이해할 수 있게 된다.
중요한 것은 사상과 추상의 언어로 이 문제를 접근하려 한 위대한 생각의 단초가 아닐까 싶다.
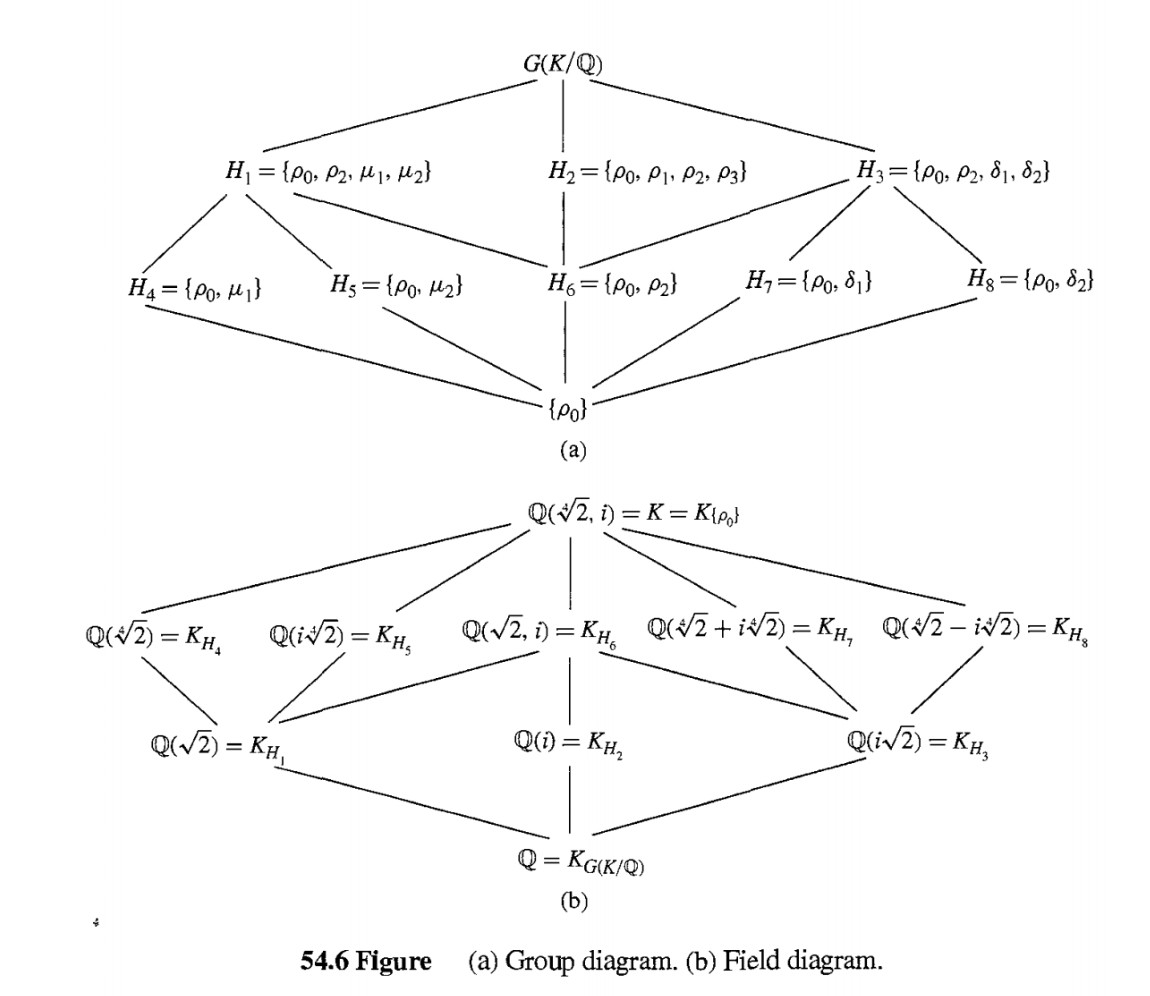
$x^4-2$ over $\mathbb{Q}$를 생각해보자. 이 다항식은 $\mathbb{Q}$ 위에서 기약이고, $\mathbb{C}$위에서 근을 가진다. normal extension field는 $K=\mathbb{Q}(\alpha=\sqrt[4]{2}, i)$이다. 이때 이 다항식의 Galois group은 $G(K/\mathbb{Q})$이고, order가 8임을 쉽게 알 수 있다. $G(K/\mathbb{Q})$의 원소는 다음 표로 정리할 수 있다.
| $i$ maps to $i$ | $i$ maps to $-i$ | ||
| $\rho_0$ | $\alpha$ maps to $\alpha$ | $\mu_1$ | $\alpha$ maps to $\alpha$ |
| $\rho_1$ | $\alpha$ maps to $i\alpha$ | $\delta_1$ | $\alpha$ maps to $-\alpha$ |
| $\rho_2$ | $\alpha$ maps to $-\alpha$ | $\mu_2$ | $\alpha$ maps to $i\alpha$ |
| $\rho_3$ | $\alpha$ maps to $-i\alpha$ | $\delta_2$ | $\alpha$ maps to $-i\alpha$ |
여기서 $\mu_1 \rho_1$과 $\rho_1 \mu_1$을 계산하면 서로 다름을 알 수 있고, 따라서 $G(K/\mathbb{Q})$는 non-abelian이다. order 8인 non-abelian group은 4th Dihedral group $D_4$과 Quaternion group $Q_8$뿐인데, $G(K/\mathbb{Q})$의 presentation이 $\left\langle a, b : a^4=b^2=e, ab=ba^{-1}\right\rangle$이니 $G(K/\mathbb{Q})\simeq D_4$임을 알 수 있다.
그리고 이때 $G(K/\mathbb{Q})$의 subgroup diagram은 다음 그림의 (a)와 같고, $K=\mathbb{Q}(\alpha, i)$의 subfield diagram은 (b)와 같다. (a)와 (b)의 diagram이 서로 뒤집힌 모양인 것을 확인할 수 있는데, Main Theorem의 (6)은 이를 의미한다. 조금만 생각해보면, $H_1\le H_2\le G(K/\mathbb{Q})$에 대해 $H_1$이 고정하는 $K$의 원소의 개수가 $H_2$가 고정하는 $K$의 원소의 개수보다 많거나 적어야 함은 당연하다. '거꾸로 뒤집힌' 모양의 diagram이 나오는 것은 이 때문이다.
사실 Main Theorem을 먼저 소개하긴 했지만, 5차 이상의 방정식의 불가해성에 대한 breakthrough는 Conjugation Isomorphism Theorem과 Isomorphic Extension Theorem이라고 생각하기 때문에 앞으로 그 내용도 포스팅할 생각이다. 내 생각을 정리할 수 있는 기회가 되었으면 한다.
- $\phi$가 G에서 G'로의 동형사상이라는 것은 $\phi$가 G에서 G'로의 일대일대응이면서 구조를 보존한다는 의미이다. 체 F와 F'에 대해 $\psi$가 둘 사이의 동형사상이라면 $\psi$는 일대일대응이면서 덧셈구조와 곱셈구조를 보존한다는 것이다. 자기 자신으로의 동형사상을 자기동형사상이라고 부른다. 더욱 자세한 내용은 검색 참고. [본문으로]
- 수학은 추상화의 학문이라고 하지만, 추상화는 구체적 예시에서부터 출발한다. 여기서도 마찬가지로, $G(K/F)$의 subgroup과 $F\le E\le K$인 intermediate field E 사이에 모종의 대칭관계가 있을 것이라는 추측은 몇 가지 구체적 예시로부터 나온 것이다. 예시가 먼저 나타난 후 정리로 일반화한 것이지, 정리로 일반화된 이후 예시를 찾은 것이 아니다. [본문으로]
'학부 수학 > 현대대수학' 카테고리의 다른 글
| Galois Theory (2). Isomorphism Extension Theorem (1) | 2024.01.04 |
|---|---|
| Galois Theory (1). Conjugate Isomorphism Theorem (0) | 2024.01.02 |
| [현대대수학] Field Extension 연습문제 풀이(Fraleigh) (0) | 2023.10.17 |
| [현대대수학] Field Extension (1) (0) | 2023.10.11 |
| [현대대수학] Sylow Theory (1) | 2023.10.11 |




